Tries, also known as prefix trees, are an easy way to encode values that share a common prefix, and easily query which values share a given prefix.
Data Structure
A Trie is a tree where the path from the root to the leaf represents a string in the dictionary.
Create Tries
At the beginning, a trie is just a root tree node.
Each time we read a string, we insert the string into the trie.
1. Let P point to the root node, and i points to the first character of the string
2. Check if s[i] is already in children list of P:
1) If yes, then move P to the child node and i ++
2) If no, create a new child node for P with the key s[i], then move P and i++
3. Repeat step 2 until you are out of characters in the string
Note that for each string, we need to add a stop value (e.g. None) as a child of the node to indicate taht the string is complete.
Examples
The following is a Trie of the string set [foo, foobar, foobaz].
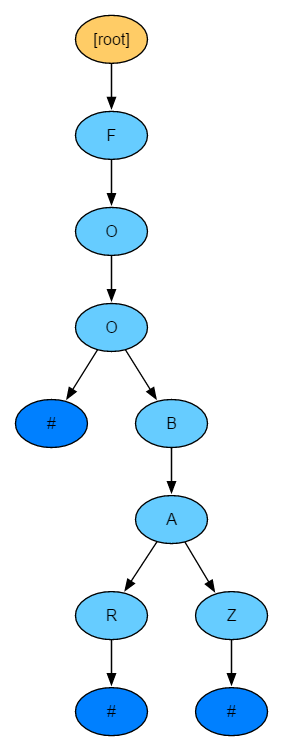
Search
Searching for a string in a trie is basically the same as inserting one,
except that instead of adding a new node when you encounter a character that isn’t encoded,
you return False indicating that the string isn’t found.
If you get to the end of the string and there’s not an indicator that this complete string exists
(a None as a child, in this example), then return False.
Otherwise, return True.
Finding all strings starting with a given prefix
Firstly, find the tree node encoding the given prefix. Then, find all leaf nodes in the subtree whose root is the found node. You can use either DFS (better is you only want to return one leaf) or BFS.
Python implementation
TrieNode
class TrieNode(object):
def __init__(self, value, string):
self.value = value
self.children = {}
self.string = string
Trie Class
class Trie(object):
"""
Class for Trie tree
"""
def __init__(self):
self.root = TrieNode(None)
def add_string(self, s):
p = self.root
for c in s:
if c in p.children:
p = p.children[c]
else:
child = TrieNode(None)
p.children[c] = child
p = child
p.word = s
def find(self, s):
p = self.root
for c in s:
if c in p.children:
p = p.children[c]
else:
return False
return p.word is not None
def start_with(self, prefix):
ret = []
p = self.root
for c in prefix:
if c in p.children:
p = p.children[c]
else:
return ret
stack = [p]
while stack:
node = stack.pop()
if node.word is not None:
ret.append(node.word)
for p in node.children.values():
stack.append(p)
return ret
Use cases
You can find all words in the set matching the given prefix or find the given word in $O(n)$ time where $n$ is the length of the word.
if __name__ == "__main__":
t = Trie()
t.add_string("foo")
t.add_string("food")
t.add_string("foot")
t.add_string("zzzdevil")
print("Start with 'f': %s" % t.start_with('f'))
There is very popular questions (FB interview question) here. The question is, by given a set of strings, find the smallest subset, which contains the prefixes for every strings in the set.
The solution is to DFS the tree, but we stop going deeper when we touch the leaf node (the node represents a word).
class Trie(object):
# ...
def smallest__subset_prefix(self):
"""
Find the smallest subset of the dictionary, which contains prefixes of all words in the dictionary
:return: a list of strings
"""
ret = []
# DFS
stack = [self.root]
while stack:
node = stack.pop()
if node.word is not None:
ret.append(node.word)
else:
for p in node.children.values():
stack.append(p)
return ret
if __name__ == "__main__":
t = Trie()
t.add_string("foo")
t.add_string("food")
t.add_string("foot")
t.add_string("zzzdevil")
print("==== Find all strings start with the given prefix ===")
prefix = "f"
print("Prefix: %s" % prefix)
print("Result: %s" % t.start_with('f'))
print()
print("==== Find smallest subset contains prefixes of all words ===")
print("Result: %s" % t.smallest__subset_prefix())
References:
https://biesnecker.com/algods/2015/04/13/dive-into-tries/
https://biesnecker.com/sweiqotd/2015/04/14/given-set-of-strings-return-minimum-subset-of-prefixes/